2019小升初数学:立体图形的计算_小升初练习题
天津奥数网 2019小升初正式进入倒计时,数学科目的复习也已经接近尾声。大家对于立体图形计算方面掌握的如何呢?下面是2019小升初数学:立体图形的计算。
一、立体图形的特征和计算公式


二、解题方法和练习题
1、正方体展开图
解题关键:利用空间想象力在脑海中将正方体展开,利用位置关系确定各个面上的字母或数字。为了防止犯错,也可以先用纸裁出正方体的展开图再进行复原,从而确定各个面上的字母或数字。
判断给定的平面图形是否属正方体表面展开图
1.1如以最长的正方形链横排为准,展开图一般是三行,个别是两行,不能是一行或四行,最长的一行(或列)在中间,可为2、3、4个,超过4个或长行不在中间的不是正方体表面展开图。如下图都不是。
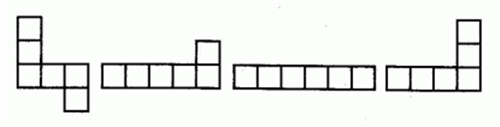
1.2在每一行(或列)的两旁,每旁只能有1个正方形与其相连,超过1个就不是。如下图都不是。
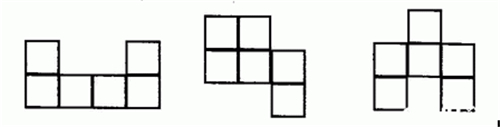
中间的长行可折作正方体侧面,它两旁(或一旁)的正方形,与中间一行相连的折作底面,不相连的再下折作侧面。
具体说可有以下4类11种图形,如作旋转或翻折后,方向会不同,但相对位置不变,这些不重复计算。
a.“一·四·一”,中间一行4个作侧面,两边各1个分别作上下底面,共有6种。
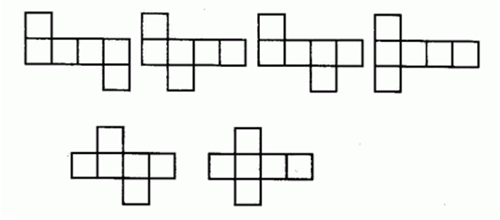
b.“二·三·一”(或一·三·二)型,中间3个作侧面,上(或下)边2个那行,相连的正方形作底面,不相连的再下折作另一个侧面,共3种。
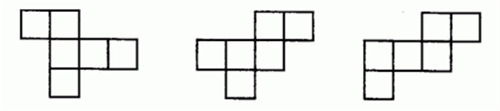
c.“二·二·二”型,成阶梯状。
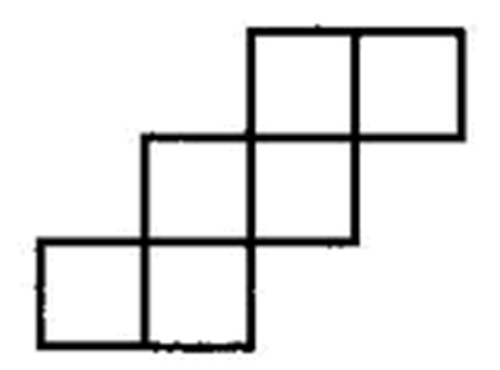
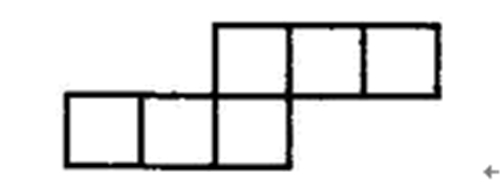
d.“三·三”型,两行只能有1个正方形相连。
例1 正方体有三种不同放置方式,问下底面各是几?
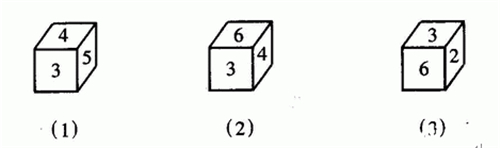
分析:先找相邻的面,余下就是相对的面。
解:上图出现最多的是3,和3相连的有2、4、5、6,余下的1就和3相对.再看6,和6相邻的有2、3、4,和3相对的是1,必和6相邻,故6和5相对,余下是4和2相对,下底面依次是2、5、1。
练习1
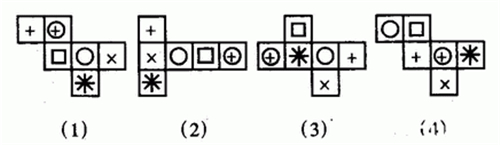
下面各图都是正方体的表面展开图,若将它们折成正方体,??则其中两个正方体各面图案完全一样,它们是().
练习2
在A、B、C内分别填上适当的数.使得它们折成正方体后,对面上的数互为倒数,则填入正方形A、B、C??的三数依次是:
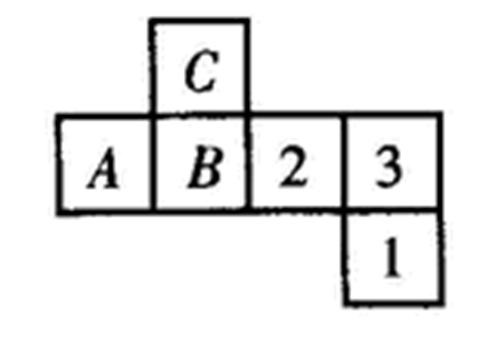
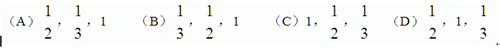
练习3
在A、B、C内分别填上适当的数,使它们折成正方体后,对面上的数互为相反数.
2、立体图形挖掉或切掉一部分求表面积和体积
解题关键:找出立体图形挖掉或切掉一部分后表面积和体积的变化以及和原来表面积和体积的关系。
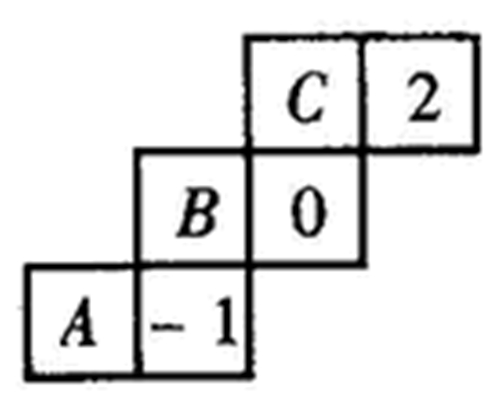
例2有一个圆柱体的零件,高10厘米,底面直径是6厘米,零件的一端有一个圆柱形的直孔,如下图.圆孔的直径是4厘米,孔深5厘米.如果将这个零件接触空气部分涂上防锈漆,一共需涂多少平方厘米?
分析解题时,既要注意圆柱体的外表面积,又要注意圆孔内的表面,同时还要注意到零件的底面是圆环.由于打孔的深度与柱体的长度不相同,所以在孔内还要有一个小圆的底面需要涂油漆,这一点不能忽略.但是,我们可以把小圆的底面与圆环拼成一个圆,即原圆柱体的底面。
解:涂漆面积:
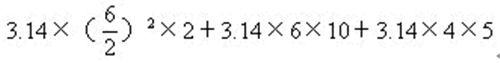
=3.14×(18+60+20)
=3.14×98=307.72(平方厘米)
答:涂油漆面积是307.72平方厘米。
练习4
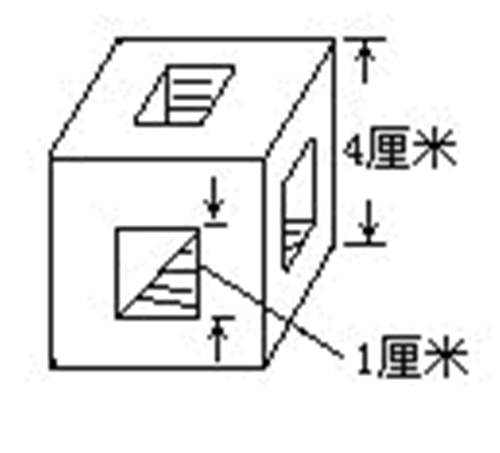
在边长为4厘米的正方体木块的每个面中心打一个边与正方体的边平行的洞。洞口是边长为1厘米的正方形,洞深1厘米(如下图)。求挖洞后木块的表面积和体积。
练习5
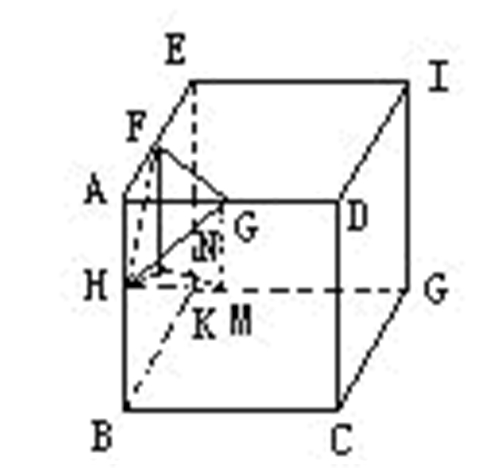
如下图是一个正方体,H、G、F分别为棱AB、AD、AE的中点。现沿三角形GFH的面锯掉一个角,问锯掉这块的体积是整个立方体体积的几分之几?
练习6
在一个棱长为50厘米的正方体木块,在它的八个角上各挖去一个棱长为5厘米的小正方体,问剩下的立体图形的表面积是多少?
3、立体图形的拼接与切割
解题关键:牢记各立体图形体积的计算公式,拼成的立体图形体积=原来各小立体图形体积之和;如果将长方体沿平行一个面的方向切下去,那么得到的2个长方体的表面积的和比原来一个大长方体的表面积多出了切口的2个面的面积。
例3一个稻谷囤,上面是圆锥体,下面是圆柱体(如下图)。圆柱的底面周长是9.42米,高2米,圆锥的高是0.6米。求这个粮囤的体积是多少立方米?
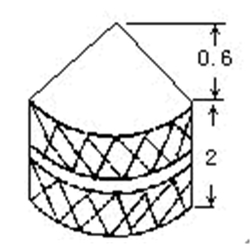
分析按一般的计算方法,先分别求出锥、柱的体积再把它们合并在一起求出总体积。但我们仔细想一想,如果把圆锥形的稻谷铺平,把它变成圆柱体,这时圆柱的高度等于0.6×=0.2(米),那么原来两个形体变成一个圆柱体,高是(2+0.2)米。这样求出变化后直圆柱的体积就可以了。
解:圆锥体化为圆柱体的高:
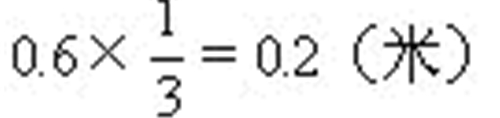
底面积:
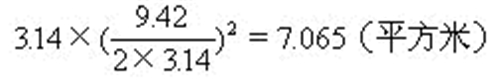
体积:
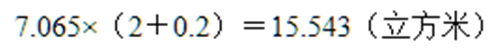
答:粮囤的体积是15.543立方米。
例4一个正方体形状的木块,棱长为1米。若沿正方体的三个方向分别锯成3份、4份和5份,如下图,共得到大大小小的长方体60块,这60块长方体的表面积的和是多少平方米?
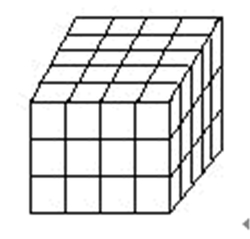
分析如果将60个长方体逐个计算表面积是个很复杂的问题,更何况锯成的小木块长、宽、高都未知使得计算小长方体的表面积成为不可能的事。如果换一个角度考虑问题:每锯一次就得到两个新的切面,这两个面的面积都等于原正方体一个面的面积,也就是,每锯一次表面积增加1+1=2平方米,这样只要计算一下锯的总次数就可使问题得到解决。
解:原正方体表面积:1×1×6=6(平方米),
一共锯了多少次:(次数比分的段数少1)
(3-1)+(4-1)+(5-1)=9(次),
表面积:6+2×9=24(平方米)。
答:60块长方体表面积的和是24平方米。
练习7
一个正方体形状的木块,棱长为1米。若沿正方体的三个方向分别锯成3份、4份和5份,如下图,共得到大大小小的长方体60块,这60块长方体的表面积的和是多少平方米?
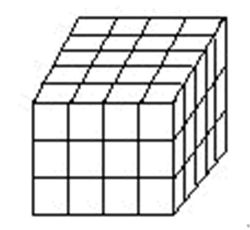
练习8
如下图所示的一个零件,中间一段是高为10厘米,底面半径为2厘米圆柱体,上端是一个半球体,下端是一个圆锥,它的高是2厘米。求这个零件的体积。

练习9
将一个长8厘米,宽6厘米,高5厘米的长方体切成两个小长方体,表面积最多增加多少平方厘米?最少增加多少平方厘米?
4、不规则物体(不溶于液体)的体积计算
解题关键:形状不规则的物体可以用排水法求得它们的体积。
(1)放入物体一个水杯,底面积为S,水的高度为h,则水的体积=Sh.当放入石头之后(石头不溶于水且全部浸没在水中),水的高度变为H,则水杯内总体积为=SH.(石头不溶于水,水上升的体积等于石头的体积。)
石头的体积=SH-Sh=S(H-h)
(2)拿出物体一个水瓶里有水和铁块(铁块全部浸没在水中),底面积为S,水的高度为H,则水瓶内总体积=SH.当拿出铁块之后,水的高度变为h,则水杯里水的体积为=Sh.(铁块不溶于水,水下降的体积等于铁块的体积。)
铁块的体积=SH-Sh=S(H-h)
例5皮球掉在一个盛有水的圆柱形水桶中。皮球的直径为12厘米,水桶底面直径为60厘米。皮球有2/3的体积浸在水中(下图)。问皮球掉进水中后,水桶的水面升高多少厘米?
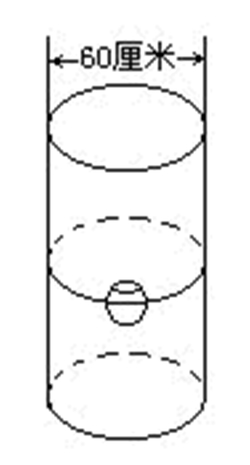
分析皮球掉进水中后排挤出一部分水,使水面升高。这部分水的体积的大小等于皮球浸在水中部分的体积,再用这个体积除以圆柱形水桶底面积,就得到水面升高的高度。
解:球的体积:
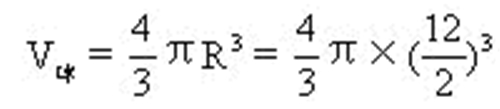
=288π(立方厘米)
水桶的底面积:π×302=900π(平方厘米)
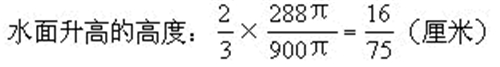

练习10
大、中、小三个正方体形的水缸都盛有缸水,它们的内边长分别为4分米、3分米、2分米。把两堆碎石分别沉浸在中、小水缸的水中,两个水池的水面分别升高了4厘米和11厘米。如果将这两堆碎石都沉浸在大水缸中,大水缸中水面将升高多少厘米?
练习11
在一只底面直径是40厘米的圆柱形盛水缸里,有一个直径是10厘米的圆锥形铸件完全浸于水中。取出铸件后,缸里的水下降0.5厘米,求铸件的高。
练习12
学校把10.5立方米的沙子铺在长6米,宽3.5米的沙坑里,铺好之后,沙子的厚度是多少?(沙子在沙坑里形成一个长方体,求厚度也就是求长方体的高)
【查看原帖并参与讨论:立体图形的计算】
编辑推荐:
2019年北辰小升初体育特长生认定的通知
2019年小升初南开中学实验班招生简章
2019年天津外国语大学附属外国语学校初中招生方案






